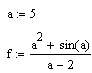Лабораторная
работа №1. Mathcad.
Базовые операции
Цель работы: получить первичные навыки работы в системе Mathcad. Изучить основные понятия и базовые операции в системе Mathcad.
Основы работы в системе Mathcad
Запустить систему математических, научных и инженерных расчетов Mathcad можно из главного меню: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad). Интерфейс Mathcad внешне напоминает интерфейс большинства приложений Windows.
Новый документ Mathcad называется Untitled (Безымянный) и получает порядковый номер. В окне редактирования формируется документ Mathcad, который желательно сразу сохранить, например, последовательностью команд File / Save as… (Файл / Сохранить как…). В открывшемся окне необходимо выбрать папку и задать имя файла. По умолчанию файлы Mathcad получают расширение .mcd.
Для ввода математических символов [цифр, знаков арифметических и логических операций, знаков математических операторов (интегралов, производных и т.д.)], греческих букв, шаблонов матриц и графиков служат палитры математических операторов и шаблонов. Они собраны на единой панели математических инструментов Math (Математическая) (рисунок 1.1), которая отображается последовательностью команд главного меню: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Рисунок 1 − Панель математических
инструментов
Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:
· формульные;
· текстовые;
· графические.
Каждая
область документа занимает прямоугольный участок, для выделения которого нужно
щелкнуть мышью в любом ее месте. Чтобы
переместить область, необходимо навести указатель мыши на ее границу и, когда
он примет вид стилизованной кисти руки, нажать на левую клавишу мыши и, не
отпуская, перетянуть выделенную область на новое место документа.
Для копирования и перемещения областей используются команды меню Edit (Правка) или стандартные комбинации клавиш операционных систем семейства Windows. Кроме того, удалить выделенную область можно комбинацией клавиш Ctrl + D, вырезать − клавишей F3, вставить − F4.
Выровнять области можно из меню Format (Формат) подменю Align Regions (Выравнивание областей) горизонтально (Across) и вертикально (Down). Отделить области поможет последовательность команд Format / Separate Regions (Формат / Отделить области).
Создание и особенности работы в формульной области
Место, с которого начинается набор формулы, указывает визир в виде красного крестика. Формульная область формируется по умолчанию и выделяется, если она активна, тонкой сплошной рамкой. Синий управляющий курсор (горизонтальная и вертикальная линии синего цвета, образующие уголок) является основным рабочим инструментом при наборе формул. Чтобы произвести операцию с объектом (сложение, умножение, возведение в степень и т. п.), необходимо выделить его синим управляющим курсором с помощью клавиш управления курсором и Пробела. Изменить направление уголка поможет клавиша Insert (Ins).
Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!
Все математические выражения в формульных областях подразделяются на определяемые (задаваемые пользователем) и вычисляемые, например:
|
|
− определяемые выражения |
|
|
− вычисляемые выражения |
Пользователь может задать выражение с использованием оператора локального присваивания «:=», который выбирается на палитре Calculator (Калькулятор) или задается комбинацией клавиш Shift + :. Для получения результата используется оператор численного вычисления «=».
В Mathcad есть два режима вычислений: ручной и автоматический. В ручном режиме для получения каждого результата нажимают клавишу F9. Установка автоматического режима осуществляется в меню Math (Математика) командой Automatic Calculation (Автоматическое вычисление).
Создание и особенности работы в текстовой области
Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо используют комбинацию клавиш Shift + ‘‘, либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.
Форматировать данные в текстовой области можно на панели инструментов Formatting (Форматирование) или в окнах форматирования текста и абзацев, вызываемых из главного меню Format (Формат) последовательностью команд Format / Text (Формат / Текст) или Format / Paragraph (Формат / Абзац) соответственно.
При возникновении проблем кодировки, связанных с набором русского текста в текстовой области, можно поступить следующим образом:
· перейти на русскую раскладку клавиатуры (RU);
· вставить текстовую область (Insert / Text Region);
· установить кириллический шрифт, например, Courier, Arial Cyr или Times New
Roman Cyr;
· набрать текст. Щелкнуть мышью вне текстовой области.
Примечание
− После удаления всех символов из текстовой области она автоматически
удаляется, и рассмотренный алгоритм надо повторять заново.
Переменные. Предопределенные
переменные
Переменные − это именованные объекты, которым присвоено некоторое значение и которые могут использоваться в выражениях путем указания их имени. Имя переменной называется идентификатором. Идентификаторы в Mathcad начинаются с буквы и могут содержать следующие символы:
· буквы любого регистра и точку «.»;
· буквы греческого алфавита;
· арабские цифры от 0 до 9;
· символы «`» − апостроф, «∞» −
бесконечность (Ctrl + Shift + Z), «_»
− подчеркивание (Shift + -), «%»
− процент (Shift + 5).
Как уже упоминалось, все выражения в формульных областях подразделяются на определяемые (задаваемые пользователем) и вычисляемые.
Для того чтобы быть использованной в вычисляемом выражении переменная должна быть определена, т. е. должна иметь некоторое значение. Попытка использовать не определенную переменную влечет появление сообщения об ошибке. Учитывая, что документ Mathcad просматривается и выполняется слева направо, сверху вниз, переменная должна быть локально определена выше и левее выражения, в котором она присутствует, в виде:
<Имя переменной> := <значение>
С помощью знака «≡» (Shift + ~ «тильда» ) производится глобальное присваивание, тогда переменная доступна из любого места документа. Однако это не всегда удобно, особенно если переменную требуется переопределять в процессе работы.
Кроме переменных, определяемых пользователем, существуют встроенные, иначе говоря, системные переменные (Build-In Variables) – это предопределенные переменные, которым изначально присвоены некоторые значения (таблица 3.1). Значения системных переменных могут быть изменены пользователем в процессе работы как присваиванием, так и в окне Math / Options на вкладке Build-In Variables (Встроенные переменные).
Таблица 1 − Некоторые
системные переменные
|
Переменная |
Значение по умолчанию |
Описание |
|
π |
3.14159… |
Число π, 15 значащих цифр |
|
e |
2.71828… |
Основание натурального логарифма, |
|
∞ |
10307 |
Бесконечность |
|
% |
0.01 |
Процент |
|
ORIGIN |
0 |
Индекс первого элемента массива |
|
TOL |
10-3 |
Допустимая погрешность численных алгоритмов |
Форматирование результатов
Под форматированием результатов понимают изменение внешнего вида выводимой на экран информации. Различают локальный (для активной области или выделенных областей) и глобальный (для всего документа) форматы результатов.
Для форматирования результатов используется вызываемое из главного меню командами Format / Result (Формат / Результат) окно, предназначенное только для форматирования вычисляемых выражений. Оно содержит вкладки: Number Format (Формат числа), Display Options (Параметры отображения), Unit Display (Отображение единиц измерения) и Tolerance (Терпимость, Допуск).
Пример к заданию 1
Задать переменные x = 2,34; y = -0,83; z = 12. Вычислить значения выражений
1) ![]() ;
;
2) ![]()
при указанных значениях переменных. Установить глобальный формат вывода результатов 4 знака после запятой и локальный формат для отдельного вычислительного блока − 5 знаков после запятой.
Решение.
Отобразим
панель математических инструментов последовательностью команд View / Toolbars / Math (Вид / Панели инструментов / Математика).
Выведем на экран палитру Calculator (Калькулятор) (рисунок 3.3) нажатием на
кнопку ![]() .
Работу удобно продолжать с использованием этой палитры.
.
Работу удобно продолжать с использованием этой палитры.

Рисунок 2 − Панель инструментов Calculator
(Калькулятор)
Напечатаем x := в месте расположения красного крестика (визира), выбрав знак присваивания на палитре Calculator (Калькулятор). В появившийся местозаполнитель введем число 2,34, используя в качестве десятичного разделителя точку:
![]()
Аналогично зададим переменные y и z, каждую в отдельном блоке.
Ввод
первого выражения начнем со знака деления ![]() с палитры Calculator, нажатие на
который вызовет появление шаблона дроби. Щелкнем левой клавишей мыши в местозаполнитель в числителе шаблона и напечатаем имя
переменной x. Для возведения в
квадрат воспользуемся значком
с палитры Calculator, нажатие на
который вызовет появление шаблона дроби. Щелкнем левой клавишей мыши в местозаполнитель в числителе шаблона и напечатаем имя
переменной x. Для возведения в
квадрат воспользуемся значком ![]() с палитры Calculator. Чтобы
продолжить набор выражения в числителе, необходимо нажать клавишу Пробел, при этом управляющий курсор
переместится таким образом, что выделенным окажется выражение x2:
с палитры Calculator. Чтобы
продолжить набор выражения в числителе, необходимо нажать клавишу Пробел, при этом управляющий курсор
переместится таким образом, что выделенным окажется выражение x2:
![]()
Введем знак «минус». Функцию синус выберем на палитре Calculator, при этом она отобразится с круглыми скобками, в которых вводится аргумент 3y. Заметьте, что знак умножения появился автоматически.
Для ввода знаменателя щелкнем левой клавишей мыши в соответствующий местозаполнитель:
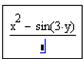
После
ввода ![]() с помощью палитры Calculator закончить
набор выражения можно, выделив с помощью клавиши Пробел всю дробь целиком синим управляющим курсором:
с помощью палитры Calculator закончить
набор выражения можно, выделив с помощью клавиши Пробел всю дробь целиком синим управляющим курсором:
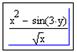
При наборе выражения 2xz не забудьте напечатать знак умножения между переменными x и z, иначе последовательность символов xz будет восприниматься как имя одной переменной:
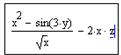
Выведем значение выражения нажатием знака равенства «=».
Для изменения формата результата щелкнем левой клавишей мыши в свободном поле документа и выполним последовательность команд Format / Result (Формат / Результат). В появившемся окне форматирования на вкладке Number Format (Формат числа) установим отображение четырех знаков после десятичного разделителя. Локальное форматирование результата производится аналогично для предварительно выбранной вычислительной формульной области:
![]()
Для
ввода второго выражения в новом формульном блоке с палитры Calculator последовательно
выбираем ![]() ,
, ![]() ,
, ![]() и
и ![]() :
:
![]()
Печатаем
единицу и знак «−». Набор квадрата косинуса в числителе и знаменателе
дроби производится в следующем порядке: выбираем cos
на палитре Calculator, в скобках
печатаем аргумент, с помощью клавиши Пробел
выделяем синим управляющим курсором косинус вместе с аргументом, только после
этого нажимаем ![]() .
Знаменатель набирается аналогично.
.
Знаменатель набирается аналогично.
Прибавить тангенс можно, выделив введенное ранее выражение синим управляющим курсором и напечатав «+». Обратите внимание, что тангенс в системе Mathcad − это tan.
Аргумент
тангенса печатается в скобках. Сначала выбирается корень, в верхний местозаполнитель вводится степень корня, затем набирается
подкоренное выражение. Для возведения тангенса в куб его выделяют курсором
вместе с аргументом, выбирают с палитры Calculator знак ![]() , в
верхний местозаполнитель вводят цифру 3.
, в
верхний местозаполнитель вводят цифру 3.
Решение полностью выглядит следующим образом:
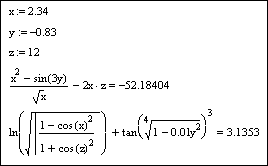
Порядок выполнения лабораторной работы
1 Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad
(Пуск / Все программы / Mathsoft Apps / Mathcad).
2 Сохранить в личной папке на диске z:\ в папке Mathcad\LAB1 новый документ с именем ФИО_1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3 Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 1
Базовые операции системы Mathcad.
4 В новой текстовой области ввести фамилию, имя, отчество и номер варианта.
Задание 1. Задать указанные переменные и вычислить значения выражений
1 и 2 из таблицы 1.
Таблица 1 − Варианты
задания 1
|
Вариант |
Значения |
Выражение 1 |
Выражение 2 |
|
1 |
x = 2,35; y = -3,83; z = 13,8 |
|
|
|
2 |
a = -0,48; b = 3,98; c = 3,08 |
|
|
|
3 |
d = -6,5; f = 0,59; g = 8 |
|
|
|
4 |
k = 6,12; n = -0,54; m = 10,5 |
|
|
|
5 |
p = 1,95; q = 0,81; r = -1,1 |
|
|
|
6 |
s = 34,1; t = -1,02; x = 1,8 |
|
|
|
7 |
u = 6,04; v = 8,1; w = 0,61 |
|
|
|
8 |
x = 2,87; y = -3,3; z = 5,25 |
|
|
|
9 |
a = 1,4; b = -0,3; c = 3,09 |
|
|
|
10 |
d = -3,84; f = 1,651; g = 15 |
|
|
|
11 |
u = 1,3419; v = -3,93; w = 12,5 |
|
|
|
12 |
x = -0,345; p = 3,883; q = 0,8 |
|
|
1 Назначение системы Mathcad.
2 Структура окна приложения Mathcad и его элементы.
3 Отображение и состав панели математических инструментов.
4 Документ Mathcad. Виды областей документа и их назначение.
5 Создание и особенности работы в формульной области.
6 Вставка, редактирование и форматирование текстовой области.
7 В чем состоит редактирование документа?
8 Переменная. Идентификатор. Правила записи идентификаторов.
9 Как задать переменную? Локальное и глобальное определения переменной.
10 Системные переменные. Как переопределить системную переменную?
11 Определяемые формульные области Mathcad.
12 Вычислительные формульные области Mathcad
13 Режимы вычислений в Mathcad.
14 Форматирование результатов.
Лабораторная
работа №1. Mathcad.
Базовые операции
Цель работы: получить первичные навыки работы в системе Mathcad. Изучить основные понятия и базовые операции в системе Mathcad.
Основы работы в системе Mathcad
Запустить систему математических, научных и инженерных расчетов Mathcad можно из главного меню: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad). Интерфейс Mathcad внешне напоминает интерфейс большинства приложений Windows.
Новый документ Mathcad называется Untitled (Безымянный) и получает порядковый номер. В окне редактирования формируется документ Mathcad, который желательно сразу сохранить, например, последовательностью команд File / Save as… (Файл / Сохранить как…). В открывшемся окне необходимо выбрать папку и задать имя файла. По умолчанию файлы Mathcad получают расширение .mcd.
Для ввода математических символов [цифр, знаков арифметических и логических операций, знаков математических операторов (интегралов, производных и т.д.)], греческих букв, шаблонов матриц и графиков служат палитры математических операторов и шаблонов. Они собраны на единой панели математических инструментов Math (Математическая) (рисунок 1.1), которая отображается последовательностью команд главного меню: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Рисунок 1 − Панель математических инструментов
Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:
· формульные;
· текстовые;
· графические.
Каждая область документа занимает прямоугольный участок, для
выделения которого нужно щелкнуть мышью в любом ее месте. Чтобы переместить область, необходимо навести
указатель мыши на ее границу и, когда он примет вид стилизованной кисти руки,
нажать на левую клавишу мыши и, не отпуская, перетянуть выделенную область на
новое место документа.
Для копирования и перемещения областей используются команды меню Edit (Правка) или стандартные комбинации клавиш операционных систем семейства Windows. Кроме того, удалить выделенную область можно комбинацией клавиш Ctrl + D, вырезать − клавишей F3, вставить − F4.
Выровнять области можно из меню Format (Формат) подменю Align Regions (Выравнивание областей) горизонтально (Across) и вертикально (Down). Отделить области поможет последовательность команд Format / Separate Regions (Формат / Отделить области).
Создание и особенности работы в
формульной области
Место, с которого начинается набор формулы, указывает визир в виде красного крестика. Формульная область формируется по умолчанию и выделяется, если она активна, тонкой сплошной рамкой. Синий управляющий курсор (горизонтальная и вертикальная линии синего цвета, образующие уголок) является основным рабочим инструментом при наборе формул. Чтобы произвести операцию с объектом (сложение, умножение, возведение в степень и т. п.), необходимо выделить его синим управляющим курсором с помощью клавиш управления курсором и Пробела. Изменить направление уголка поможет клавиша Insert (Ins).
Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!
Все математические выражения в формульных областях подразделяются на определяемые (задаваемые пользователем) и вычисляемые, например:
|
|
− определяемые выражения |
|
|
− вычисляемые выражения |
Пользователь может задать выражение с использованием оператора локального присваивания «:=», который выбирается на палитре Calculator (Калькулятор) или задается комбинацией клавиш Shift + :. Для получения результата используется оператор численного вычисления «=».
В Mathcad есть два режима вычислений: ручной и автоматический. В ручном режиме для получения каждого результата нажимают клавишу F9. Установка автоматического режима осуществляется в меню Math (Математика) командой Automatic Calculation (Автоматическое вычисление).
Создание и особенности работы в
текстовой области
Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо используют комбинацию клавиш Shift + ‘‘, либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.
Форматировать данные в текстовой области можно на панели инструментов Formatting (Форматирование) или в окнах форматирования текста и абзацев, вызываемых из главного меню Format (Формат) последовательностью команд Format / Text (Формат / Текст) или Format / Paragraph (Формат / Абзац) соответственно.
При возникновении проблем кодировки, связанных с набором русского текста в текстовой области, можно поступить следующим образом:
· перейти на русскую раскладку клавиатуры (RU);
· вставить текстовую область (Insert / Text Region);
· установить кириллический шрифт, например, Courier, Arial Cyr или Times New
Roman Cyr;
· набрать текст. Щелкнуть мышью вне текстовой области.
Примечание −
После удаления всех символов из текстовой области она автоматически удаляется,
и рассмотренный алгоритм надо повторять заново.
Переменные. Предопределенные
переменные
Переменные − это именованные объекты, которым присвоено некоторое значение и которые могут использоваться в выражениях путем указания их имени. Имя переменной называется идентификатором. Идентификаторы в Mathcad начинаются с буквы и могут содержать следующие символы:
· буквы любого регистра и точку «.»;
· буквы греческого алфавита;
· арабские цифры от 0 до 9;
· символы «`» − апостроф, «∞» −
бесконечность (Ctrl + Shift + Z), «_» − подчеркивание (Shift + -), «%» − процент (Shift + 5).
Как уже упоминалось, все выражения в формульных областях подразделяются на определяемые (задаваемые пользователем) и вычисляемые.
Для того чтобы быть использованной в вычисляемом выражении переменная должна быть определена, т. е. должна иметь некоторое значение. Попытка использовать не определенную переменную влечет появление сообщения об ошибке. Учитывая, что документ Mathcad просматривается и выполняется слева направо, сверху вниз, переменная должна быть локально определена выше и левее выражения, в котором она присутствует, в виде:
<Имя
переменной> := <значение>
С помощью знака «≡» (Shift + ~ «тильда» ) производится глобальное присваивание, тогда переменная доступна из любого места документа. Однако это не всегда удобно, особенно если переменную требуется переопределять в процессе работы.
Кроме переменных, определяемых пользователем, существуют встроенные, иначе говоря, системные переменные (Build-In Variables) – это предопределенные переменные, которым изначально присвоены некоторые значения (таблица 3.1). Значения системных переменных могут быть изменены пользователем в процессе работы как присваиванием, так и в окне Math / Options на вкладке Build-In Variables (Встроенные переменные).
Таблица 1 − Некоторые системные переменные
|
Переменная |
Значение по умолчанию |
Описание |
|
π |
3.14159… |
Число π, 15 значащих цифр |
|
e |
2.71828… |
Основание
натурального логарифма, |
|
∞ |
10307 |
Бесконечность |
|
% |
0.01 |
Процент |
|
ORIGIN |
0 |
Индекс первого элемента массива |
|
TOL |
10-3 |
Допустимая погрешность численных алгоритмов |
Форматирование результатов
Под форматированием результатов понимают изменение внешнего вида выводимой на экран информации. Различают локальный (для активной области или выделенных областей) и глобальный (для всего документа) форматы результатов.
Для форматирования результатов используется вызываемое из главного меню командами Format / Result (Формат / Результат) окно, предназначенное только для форматирования вычисляемых выражений. Оно содержит вкладки: Number Format (Формат числа), Display Options (Параметры отображения), Unit Display (Отображение единиц измерения) и Tolerance (Терпимость, Допуск).
Пример к заданию 1
Задать переменные x = 2,34; y = -0,83; z = 12. Вычислить значения выражений
1) ![]() ;
;
2) ![]()
при указанных значениях переменных. Установить глобальный формат вывода результатов 4 знака после запятой и локальный формат для отдельного вычислительного блока − 5 знаков после запятой.
Решение.
Отобразим панель математических инструментов
последовательностью команд View / Toolbars / Math (Вид / Панели инструментов / Математика).
Выведем на экран палитру Calculator (Калькулятор) (рисунок 3.3) нажатием на
кнопку ![]() . Работу
удобно продолжать с использованием этой палитры.
. Работу
удобно продолжать с использованием этой палитры.

Рисунок 2 − Панель инструментов Calculator (Калькулятор)
Напечатаем x := в месте расположения красного крестика (визира), выбрав знак присваивания на палитре Calculator (Калькулятор). В появившийся местозаполнитель введем число 2,34, используя в качестве десятичного разделителя точку:
![]()
Аналогично зададим переменные y и z, каждую в отдельном блоке.
Ввод первого выражения начнем со знака деления ![]() с палитры Calculator, нажатие на
который вызовет появление шаблона дроби. Щелкнем левой клавишей мыши в местозаполнитель в числителе шаблона и напечатаем имя переменной
x. Для возведения в квадрат воспользуемся значком
с палитры Calculator, нажатие на
который вызовет появление шаблона дроби. Щелкнем левой клавишей мыши в местозаполнитель в числителе шаблона и напечатаем имя переменной
x. Для возведения в квадрат воспользуемся значком ![]() с палитры Calculator. Чтобы
продолжить набор выражения в числителе, необходимо нажать клавишу Пробел, при этом управляющий курсор
переместится таким образом, что выделенным окажется выражение x2:
с палитры Calculator. Чтобы
продолжить набор выражения в числителе, необходимо нажать клавишу Пробел, при этом управляющий курсор
переместится таким образом, что выделенным окажется выражение x2:
![]()
Введем знак «минус». Функцию синус выберем на палитре Calculator, при этом она отобразится с круглыми скобками, в которых вводится аргумент 3y. Заметьте, что знак умножения появился автоматически.
Для ввода знаменателя щелкнем левой клавишей мыши в соответствующий местозаполнитель:
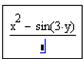
После ввода ![]() с помощью палитры Calculator закончить набор выражения можно, выделив с помощью
клавиши Пробел всю дробь целиком синим
управляющим курсором:
с помощью палитры Calculator закончить набор выражения можно, выделив с помощью
клавиши Пробел всю дробь целиком синим
управляющим курсором:
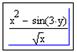
При наборе выражения 2xz не забудьте напечатать знак умножения между переменными x и z, иначе последовательность символов xz будет восприниматься как имя одной переменной:
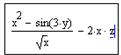
Выведем значение выражения нажатием знака равенства «=».
Для изменения формата результата щелкнем левой клавишей мыши в свободном поле документа и выполним последовательность команд Format / Result (Формат / Результат). В появившемся окне форматирования на вкладке Number Format (Формат числа) установим отображение четырех знаков после десятичного разделителя. Локальное форматирование результата производится аналогично для предварительно выбранной вычислительной формульной области:
![]()
Для ввода второго выражения в новом формульном блоке с
палитры Calculator последовательно выбираем ![]() ,
, ![]() ,
, ![]() и
и ![]() :
:
![]()
Печатаем единицу и знак «−». Набор квадрата косинуса в
числителе и знаменателе дроби производится в следующем порядке: выбираем cos на палитре Calculator, в скобках печатаем аргумент, с помощью клавиши Пробел выделяем синим управляющим
курсором косинус вместе с аргументом, только после этого нажимаем ![]() .
Знаменатель набирается аналогично.
.
Знаменатель набирается аналогично.
Прибавить тангенс можно, выделив введенное ранее выражение синим управляющим курсором и напечатав «+». Обратите внимание, что тангенс в системе Mathcad − это tan.
Аргумент тангенса печатается в скобках. Сначала выбирается
корень, в верхний местозаполнитель вводится степень
корня, затем набирается подкоренное выражение. Для возведения тангенса в куб
его выделяют курсором вместе с аргументом, выбирают с палитры Calculator знак ![]() , в
верхний местозаполнитель вводят цифру 3.
, в
верхний местозаполнитель вводят цифру 3.
Решение полностью выглядит следующим образом:
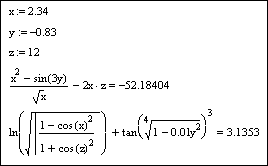
Порядок выполнения лабораторной работы
5 Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad
(Пуск / Все программы / Mathsoft Apps / Mathcad).
6 Сохранить в личной папке на диске z:\ в папке Mathcad\LAB1 новый документ с именем ФИО_1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
7 Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 1
Базовые операции системы Mathcad.
8 В новой текстовой области ввести фамилию, имя, отчество и номер варианта.
Задание 1.
Задать указанные переменные и вычислить значения выражений 1 и 2 из таблицы 1.
Таблица 1 − Варианты задания 1
|
Вариант |
Значения |
Выражение 1 |
Выражение 2 |
|
1 |
x = 2,35; y = -3,83; z = 13,8 |
|
|
|
2 |
a = -0,48; b = 3,98; c = 3,08 |
|
|
|
3 |
d = -6,5; f = 0,59; g = 8 |
|
|
|
4 |
k = 6,12; n = -0,54; m = 10,5 |
|
|
|
5 |
p = 1,95; q = 0,81; r = -1,1 |
|
|
|
6 |
s = 34,1; t = -1,02; x = 1,8 |
|
|
|
7 |
u = 6,04; v = 8,1; w = 0,61 |
|
|
|
8 |
x = 2,87; y = -3,3; z = 5,25 |
|
|
|
9 |
a = 1,4; b = -0,3; c = 3,09 |
|
|
|
10 |
d = -3,84; f = 1,651; g = 15 |
|
|
|
11 |
u = 1,3419; v = -3,93; w = 12,5 |
|
|
|
12 |
x = -0,345; p = 3,883; q = 0,8 |
|
|
Контрольные вопросы
15 Назначение системы Mathcad.
16 Структура окна приложения Mathcad и его элементы.
17 Отображение и состав панели математических инструментов.
18 Документ Mathcad. Виды областей документа и их назначение.
19 Создание и особенности работы в формульной области.
20 Вставка, редактирование и форматирование текстовой области.
21 В чем состоит редактирование документа?
22 Переменная. Идентификатор. Правила записи идентификаторов.
23 Как задать переменную? Локальное и глобальное определения переменной.
24 Системные переменные. Как переопределить системную переменную?
25 Определяемые формульные области Mathcad.
26 Вычислительные формульные области Mathcad
27 Режимы вычислений в Mathcad.
28 Форматирование результатов.
Лабораторная
работа №2. Mathcad.
Функции. Ранжированные переменные. Графики
Цель работы: Изучить использование встроенных функций, способы задания и использования ранжированной переменной, способы создания и форматирования графиков в системе Mathcad.
Функции
Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя.
Встроенные функции
изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры,
обычно в нижнем регистре. Полный перечень встроенных функций можно получить,
выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку ![]() панели инструментов. При этом появляется окно,
где справа перечислены возможные категории функций, а слева – список функций из
выделенной категории.
панели инструментов. При этом появляется окно,
где справа перечислены возможные категории функций, а слева – список функций из
выделенной категории.
Среди наиболее часто используемых функций можно указать:
· sin(z) − синус z (z задается в радианах);
· cos(z) −
косинус z;
· tan(z) −
тангенс z;
· cot(z) −
котангенс z;
· exp(z) – экспоненциальная функция, значение е (основание натурального логарифма) в степени z;
· ln(z) – натуральный логарифм z;
· log(z) – десятичный логарифм числа z;
· log(z, b) – логарифм числа z по основанию b;
· acos(z) – арккосинус z;
· acot(z) – арккотангенс z;
· asin(z) – арксинус z;
· atan(z) – арктангенс z;
· round(z, n)
– при n > 0
возвращает округленное значение z с точностью до n знаков после десятичной точки. При n < 0 возвращает
округленное значение z
с n цифрами
слева от десятичной точки. При n = 0 или при использовании функции без второго
аргумента возвращает значение z, округленное до
ближайшего целого;
· trunc(z) – целая часть числа z;
· rnd(x) – функция генерации случайных чисел, равномерно
распределенных от 0 до х;
· mod(n, k) – возвращает остаток от деления n на k, причем аргументы могут быть
действительными, а результат имеет тот же знак, что и n.
· if(cond, x,
у) – функция условия, возвращает
выражение х,
если условие cond
истинно (не равно 0), и выражение у в
остальных случаях.
Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется
Имя(список аргументов) := Выражение
Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.
Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.
Ранжированные
(дискретные) переменные
В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.
Ранжированная переменная общего вида определяется выражением:
Имя := x1, x2 .. xn
Здесь
· Имя –
задаваемое пользователем имя ранжированной переменной;
· x1 – первое значение ранжированной переменной;
· x2 – второе значение ранжированной переменной (x2 = x1 + Dx − первое значение плюс шаг);
· xn – последнее значение ранжированной переменной.
Значения x1 и x2 разделяются запятой, двоеточие представляет
собой единый оператор, указывающий на изменение переменной в заданных пределах.
Он вводится с клавиатуры клавишей «;»
или выбирается с палитры математических инструментов Matrix
(кнопка ![]() − Range Variable).
− Range Variable).
Например, если переменная изменяется в интервале ![]() с шагом
с шагом ![]() , то она задается в виде
, то она задается в виде
![]()
Можно определить и обобщенно:
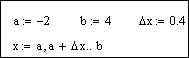
Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1. Если x1 > x2, то шаг – отрицательный. Существует сокращенная форма определения ранжированной переменной:
Имя := x1 .. xn
В этом случае шаг изменения ранжированной переменной по умолчанию равен 1 или -1 (если x1 > x2).
Любое выражение с ранжированной переменной создает после знака равенства «=» таблицу вывода. Числа в таблицах можно форматировать с помощью окна Result Format (Формат Результата).
Ранжированные переменные используются при выполнении циклических (повторяющихся) вычислений, для вывода чисел и численных значений функций в виде таблиц, построения графиков функций, задания массивов.
Построение графиков функций
Основные
типы графиков в Mathcad
Основные типы графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График) (рисунок 1) или в подменю Graph главного меню Insert (Вставка).

Рисунок 1
− Панель инструментов для работы с графиками
Имеется семь основных шаблонов графиков:
· X-Y Plot
(Декартов график) – двумерный график в декартовой прямоугольной системе
координат;
· Polar Plot
(Полярный график) – двумерный график в полярных координатах;
· Surface Plot
(График поверхности) – график поверхности в трехмерном пространстве;
· Contour Plot
(Контурный график) – график линий одного уровня;
· 3D Scatter Plot (Точечный график) – множество точек в трехмерном пространстве;
· 3D Bar Plot (Трехмерная гистограмма) – изображение функции в виде
совокупности параллелепипедов в трехмерном пространстве;
· Vector Field Plot (Векторное поле) – плоский векторный график.
Еще один тип графиков, не выведенный на палитру Graph − это Patch Plot, лоскутный график поверхности, который можно задать при форматировании трехмерных графиков.
Для форматирования графиков служат следующие команды из подменю Graph (График) пункта главного меню Format (Формат):
· X-Y Plot –
изменение формата двумерного графика в декартовой системе координат;
· Polar Plot –
изменение формата графика в полярных координатах;
· 3D Plot –
изменение формата трехмерного графика.
Дополнительными инструментами более детального исследования графиков функций являются трассировка и масштабирование:
· Trace (значок ![]() ) –
отслеживание координат точек графика;
) –
отслеживание координат точек графика;
· Zoom (значок ![]() ) –
изменение размеров отдельных участков плоскости графика.
) –
изменение размеров отдельных участков плоскости графика.
Эти инструменты можно найти на палитре Graph (График) или вызвать последовательным выбором из главного меню Format / Graph / Trace… (или Zoom…) – Формат / График / Трассировка… (или Масштаб…).
График функции в декартовой системе координат
Для построения графиков функций одной переменной в декартовой системе координат в Mathcad предусмотрены способы: упрощенный («быстрый»), с использованием ранжированной переменной, по массивам данных.
Для построения двумерного графика
достаточно вызвать шаблон X-Y Plot ![]() , в
знакоместо по оси абсцисс вписать имя переменной, а в знакоместо по оси ординат
вписать функцию и щелкнуть левой клавишей мыши. При этом многие параметры
задаются автоматически, например, пределы изменения аргумента устанавливаются
от минус 10 до 10 или от 0 до 10.
, в
знакоместо по оси абсцисс вписать имя переменной, а в знакоместо по оси ординат
вписать функцию и щелкнуть левой клавишей мыши. При этом многие параметры
задаются автоматически, например, пределы изменения аргумента устанавливаются
от минус 10 до 10 или от 0 до 10.
Примечание − Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.
Система Mathcad дает возможность построения графиков по данным, представленным векторами, матрицами или таблицами данных, что бывает необходимо при решении ряда прикладных задач. Для этого достаточно задать массивы и вписать их имена в соответствующие знакоместа шаблона:
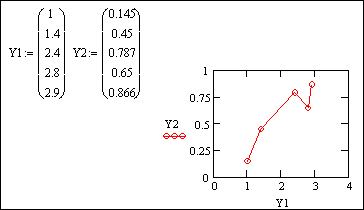
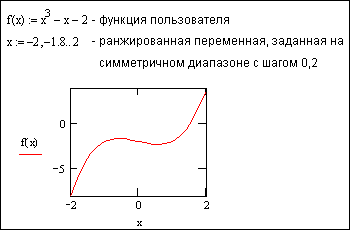
Большие возможности предоставляет поэтапное построение графиков с использованием ранжированной переменной:
1) определяется функция пользователя;
2) задается ранжированная переменная на некотором диапазоне с требуемым шагом;
3) вставляется шаблон графика;
4) в соответствующие знакоместа вводятся имена аргумента и функции.
Например, построение графика
функции ![]() будет выглядеть
следующим образом:
будет выглядеть
следующим образом:
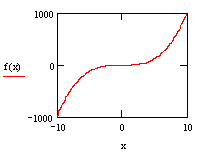
Каждый из описанных способов имеет свои преимущества и недостатки. Так, построенные упрощенным способом графики ввиду автоматически выбранных границ отображения могут не отражать существенные особенности функции. Устранить возникший недочет можно, уменьшив пределы изменения аргумента или функции (рисунок 2.5).
|
|
Рисунок
2.5 − График с большими пределами построения и окончательно
отформатированный график
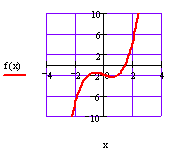
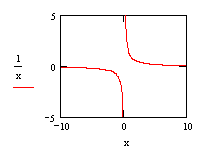
Использование ранжированной переменной позволяет варьировать шаг между узловыми точками графика от значительного (для построения диаграмм и точечных зависимостей) до мелкого (для более точного отображения непрерывных зависимостей). Но при данном способе возможно появление ошибок при построении функций с особенностями или ограниченной областью определения. На рисунке 2.6 слева представлен график, построенный «быстрым» способом, а справа – ошибочный, с помощью ранжированной переменной.
|
|
Рисунок
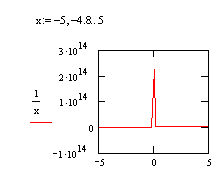
2.6 − Способы построения графика функции y = 1/x
Форматирование
двумерных графиков
Для изменения формата уже построенного графика необходимо сначала активизировать соответствующую графическую область, щелкнув левой клавишей мыши в поле графика. Перемещение, копирование, изменение размеров графической области выполняется согласно общим для областей Mathcad правилам.
Окно форматирования текущего графика функции в декартовой системе координат (Formatting Currently Selected X-Y Plot) можно вызвать одним из следующих способов:
· последовательностью команд главного
меню Format / Graph / X-Y Plot… (Формат
Декартовых графиков...);
· двойным щелчком левой клавишей мыши в
области графика;
· щелчком правой клавишей мыши в
графической области с последующим выбором из контекстного меню команды Format…
Диалоговое окно форматирования имеет четыре вкладки:
· X-Y Axes
(X-Y Оси) – изменение параметров осей;
· Traces (Тип линий) – изменение линий
графика;
· Labels (Метки) – управление надписями на
графике;
· Defaults (По умолчанию) – задание опций по
умолчанию.
На вкладке X-Y Axes (рисунок 2.7) содержатся следующие опции, относящиеся к оси абсцисс и оси ординат, соответственно поля Х-Axis и Y-Axis:
· Log Scale (Логарифмическая шкала) – установка
логарифмического масштаба, полезного в случае различия данных на несколько
порядков;
· Grid Lines (Сетка) – установка вспомогательных
линий сетки;
· Numbered (Нумерация) – установка числовых
данных по осям. Если флажок снят, то числовые данные не отображаются;
· Autoscale (Автоматическая шкала) – автоматическое масштабирование,
выбор диапазона осей производится процессором Mathcad;
· Show Markers (Показать отметки) – установка
вспомогательных линий-маркеров. При выборе этой опции вдоль соответствующей оси
появляются два знакоместа, позволяющие вводить числовые данные. Эти данные
отобразятся в виде подписи на пунктирной линии-маркере, пересекающей
графическую область перпендикулярно выбранной оси;
· Auto Grid (Автосетка)
– автоматическая установка вспомогательных линий сетки производится процессором
Mathcad. Для установки желаемого количества линий флажки необходимо
снять;
· Number of Grids (Число линий) – установка
необходимого числа вспомогательных линий сетки.

Рисунок
2.7 − Вкладка форматирования осей графика
В поле Axes Style (Стиль осей координат) расположены следующие переключатели, регулирующие отображение координатных осей:
· Boxed (В рамке) – прямоугольное обрамление графика линиями,
выполняющими функцию осей координат;
· Crossed (Только оси) – отображение осей в виде прямых,
пересекающихся в начале координат;
· None (Нет) – отсутствие осей.
Флажком Equal Scales (Равны), устанавливаются равные масштабы по осям.
Следующая второй вкладка Traces (Тип линий) служит для управления отображением линий графика. С помощью опций этой вкладки можно регулировать следующие параметры (рисунок 2.8):
· Legend Label
(Надпись легенды, Метка) – текст, описывающий ряд данных, имя линии графика;
· Symbol (Символ) – выбор символа, которым отображаются
узловые точки данных (для которых вычисляются координаты) на графике;
· Line (Линия) – установка стиля линий (сплошная, пунктирная
и т. п.);
· Color (Цвет) – цвет линий и узловых точек данных;
· Type (Тип) – тип представления графиков;
· Weight (Толщина) – толщина линии и точек данных.
Приступая к форматированию линии графика, выберите щелчком мыши необходимую строку из представленного в окне форматирования списка, данные в котором расположены в соответствии с порядком следования функций по оси ординат.
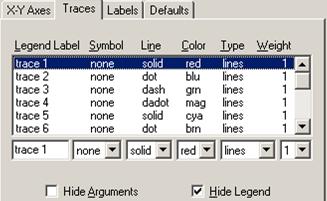
Рисунок
2.8 Вкладка форматирования линий графика
Раскрывающийся список Symbol (Символ) предлагает следующие маркеры для узловых точек графика выбранной функции:
· none – без маркера;
· ×’s – крестик;
· +’s – плюс;
· box – квадрат;
· dmnd – ромб;
· o’s – окружность.
Раскрывающийся список Line (Линия) позволяет выбрать один из следующих стилей отображения линий:
· solid – сплошная;
· dot – пунктир;
· dash – штрих;
· dadot – штрих-пунктир.
Раскрывающийся список Color (Цвет) содержит основные цвета линий и узловых точек.
Для установки типа графика имеются следующие возможности, перечисленные в раскрывающемся списке Type (Тип):
· lines (линия) – построение линиями;
· points (точки) – построение точками;
· error (ошибки) – построение вертикальными черточками с
оценкой интервала погрешностей;
· bar (столбцы) – построение в виде гистограммы;
· step (шаг) – построение ступенчатой линией;
· draw (рисовать) – проводятся линии от точки до точки;
· stem (стержень) – построение вертикальными линиями от оси
абсцисс до узловых точек;
· solid bar
(сплошные столбцы) – построение в виде гистограммы с закрашенными столбцами.
Еще два параметра вкладки Traces связаны с возможностью отображения на графике вспомогательных надписей:
· Hide Arguments
(Скрыть аргументы) – при установленном флажке математические выражения по осям
графика не отображаются;
· Hide legend
(Скрыть легенду) – при установленном флажке имена линий графиков не
отображаются.
Третья вкладка окна форматирования Label (Метки) служит для установки отображения дополнительных надписей:
· Title (Заголовок) – название графика;
· X-Axis (Х-ось) –
надпись по оси абсцисс;
· Y-Axis (Y-ось) –
надпись по оси ординат;
В поле Title вкладки Label (Метки) содержатся переключатели Above (Сверху) и Below (Снизу) и флажок Show Title (Показать заголовок), управляющие отображением титульной надписи.
Вкладка Defaults (По умолчанию) служит для задания параметров графики по умолчанию:
· Change to Defaults – вернуть значения по
умолчанию;
· Use for Defaults – использовать далее в
документе параметры текущего графика в качестве значений по умолчанию.
Обычно форматирование графика предусматривает множественные преобразования. Поэтому для просмотра влияния отдельных установок или для назначения большинства параметров без закрытия диалогового окна следует нажимать кнопку Apply (Применить).
Пример к заданию 1
Вычислить значения функции ![]() при b1 = 1,3;
при b1 = 1,3; ![]() ;
; ![]()
Решение.
Начнем выполнение задания с присваивания значения константе b1. Для этого напечатаем b1 := 1.3, выбрав знак «:=» на палите Calculator в нижнем левом углу.
Введем выражение для искомой функции следующим образом:
![]()
Для этого сначала напечатаем ![]() . Черту дроби поставим нажатием на клавишу деление «/»
на клавиатуре или щелчком по соответствующей кнопке на палитре Calculator. Далее наведем стрелку мыши на числитель дроби и
щелкнем левой клавишей для установки там управляющего курсора.
. Черту дроби поставим нажатием на клавишу деление «/»
на клавиатуре или щелчком по соответствующей кнопке на палитре Calculator. Далее наведем стрелку мыши на числитель дроби и
щелкнем левой клавишей для установки там управляющего курсора.
Щелкнем по кнопке ![]() на палитре Calculator
и напечатаем квадратный корень из переменной x. Наведем
стрелку мыши на знаменатель дроби и щелчком левой клавишей мыши переместим туда
курсор. Функцию cot − котангенс − можно
напечатать на клавиатуре, а можно выбрать из списка в окне Insert Function (Вставка функции),
отображаемом нажатием на клавишу
на палитре Calculator
и напечатаем квадратный корень из переменной x. Наведем
стрелку мыши на знаменатель дроби и щелчком левой клавишей мыши переместим туда
курсор. Функцию cot − котангенс − можно
напечатать на клавиатуре, а можно выбрать из списка в окне Insert Function (Вставка функции),
отображаемом нажатием на клавишу ![]() на панели инструментов или комбинацией клавиш Ctrl + E. Не удаляя появившиеся
скобки, напечатаем x:
на панели инструментов или комбинацией клавиш Ctrl + E. Не удаляя появившиеся
скобки, напечатаем x:
![]()
Для возведения в квадрат котангенса выделим управляющим курсором
выражение cot(x) вместе с аргументом, используя для этого стрелки
перемещения по тексту или клавишу Пробел,
и нажмем значок ![]() :
:
![]()
Для завершения ввода выражения в знаменателе нажмем Пробел и напечатаем +b1.
Зададим пределы изменения аргумента m. Для этого щелкнем мышью в пустом месте документа и напечатаем
m:= -2, -1.4
Далее, не перемещая курсор, нажмем на панели Matrix (Матрицы)
значок ![]() (клавиша «;»
клавиатуры) и после появления двоеточия (многоточия) наберем последнее значение
5.
(клавиша «;»
клавиатуры) и после появления двоеточия (многоточия) наберем последнее значение
5.
Для получения таблицы вывода значений переменной m напечатаем с клавиатуры m = . Знак «=» можно также найти на палитре Calculator в правом нижнем углу. Наберем fun1(m) = на клавиатуре. В результате появится таблица вывода значений функции fun1 на заданном промежутке.
Для построения графика функции вставим графическую область
нажатием на значок вставки двумерного графика X-Y Plot ![]() на палитре Graph (График). В нижний местозаполнитель
введем имя переменной m, а в местозаполнитель
по оси ординат введем имя функции с аргументом в скобках fun1(m). Щелкнем левой клавишей мыши вне
графической области.
на палитре Graph (График). В нижний местозаполнитель
введем имя переменной m, а в местозаполнитель
по оси ординат введем имя функции с аргументом в скобках fun1(m). Щелкнем левой клавишей мыши вне
графической области.
Форматирование
графика осуществляется в окне, вызываемом щелчком правой клавишей мыши в
графической области и выбором из контекстного меню команды Format.
Установим пересечение осей выбором переключателя Crossed (Только оси). Отображение вспомогательных линий задается установкой флажков по осям X и Y в строке Grid Lines (Вспомогательные линии).
Порядок и результаты выполнения задания в пакете Mathcad:
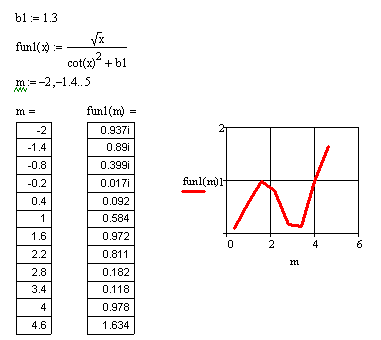
Примечание − При выполнении задания использовалась функция fun1 с формальным параметром х. При обращении к этой функции формальный параметр заменяется фактическим параметром m. Следует помнить, что документ Mathcad выполняется сверху вниз. Поэтому сначала следует задать переменную m, а затем ниже использовать выражение для искомой функции с этой переменной.
Порядок выполнения лабораторной работы
9 Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad
(Пуск / Все программы / Mathsoft Apps / Mathcad).
10 Сохранить в личной папке на диске z:\ в папке Mathcad\LAB2 новый документ с именем ФИО_2, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
11 Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 2
Система Mathcad.
Функции. Ранжированные переменные. Графики.
12 В новой текстовой области ввести фамилию, имя, отчество и номер варианта.
Задание 1. Задать ранжированную переменную и вычислить значения функции при изменении аргумента с постоянным шагом (таблица 1). Построить и отформатировать график функции.
Таблица1 − Варианты задания 1
|
Вариант |
Переменная |
Функция |
Вариант |
Переменная |
Функция |
|
1 |
|
|
7 |
|
|
|
2 |
|
|
8 |
|
|
|
3 |
|
|
9 |
|
|
|
4 |
|
|
10 |
|
|
|
5 |
|
|
11 |
|
|
|
6 |
|
|
12 |
|
|
Контрольные вопросы
29 Что понимают под встроенной функцией?
30 Как задать встроенную функцию?
31 Перечислить основные категории встроенных функций.
32 Что такое функция пользователя и как она задается?
33 Как обратиться к функции пользователя?
34 Что такое ранжированная переменная и как она задается? Правила записи ранжированной переменной.
35 Что такое шаг изменения ранжированной переменной? С каким шагом изменяется ранжированная переменная, если задать только начальное и конечное значения?
36 С каким шагом изменяется ранжированная переменная, если начальное значение больше конечного?
37 Типы графиков в Mathcad. Способы создания графиков в декартовой системе координат.
38 Форматирование графиков. Содержание вкладок окна форматирования графика в декартовой системе координат
Лабораторная работа №3. Mathcad.
Массивы
Цель работы: изучить способы создания и использования массивов, основные векторные и матричные операции и функции в системе Mathcad.
Массивы
Основные
определения. Способы создания массивов
Массив в пакете Mathcad − это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя.
Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные. Различают векторы-строки (матрицы 1×n) и векторы-столбцы (матрицы m×1), которые дают разные результаты при векторных и матричных операциях, например:
![]() – вектор-столбец;
– вектор-столбец; ![]() – вектор-строка.
– вектор-строка.
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Нижняя граница индексации (другими словами, номер первого элемента массива) определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:
|
ORIGIN:=1 |
Существует несколько способов создания массивов.
1-й способ. Использование специальной панели Insert Matrix (Вставка матрицы) (рисунок 1).
Сначала набирается имя массива и оператор присваивания, например,
![]()
Далее можно выполнить одно из перечисленных ниже действий:
1.1 воспользоваться командой Matrix... (Матрица...) пункта главного меню Insert (Вставка);
1.2 нажать комбинацию клавиш Ctrl + M;
1.3 щелкнуть по пиктограмме с изображением шаблона матрицы с одноименной палитры математических инструментов Matrix (Матрица).
Рисунок 1 − Панель математических
инструментов и палитра для работы с векторами и матрицами
Любое из этих действий вызывает появление диалогового окна (рисунок 2), в котором надо указать количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.
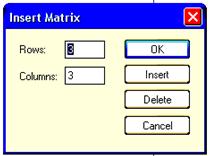
Рисунок 2 − Диалоговое окно вставки
шаблона матрицы
На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:
Переход к следующему знакоместу производится нажатием клавиши Tab или с помощью клавиш управления курсором.
2-й способ. Использование ранжированной переменной.
Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:
1) определяется системная переменная ORIGIN;
2) задается ранжированная переменная (переменные) для нумерации элементов;
3) индексированной переменной присваиваются значения элементов массива через запятую или в виде явной формулы.
Обращаться
к отдельным элементам вектора или матрицы можно, используя нижний индекс,
принимающий только целочисленные значения. Для ввода нижнего индекса после
имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка)
либо используется пиктограмма ![]() с палитры математических инструментов Matrix (рисунок 1). Для
элемента матрицы указываются через запятую два индекса, обозначающих номер
строки и номер столбца соответственно.
с палитры математических инструментов Matrix (рисунок 1). Для
элемента матрицы указываются через запятую два индекса, обозначающих номер
строки и номер столбца соответственно.
Операторы
для работы с векторами и матрицами
Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.
Таблица 1 − Команды
палитры инструментов Matrix (Матрица)
|
Команда |
Описание |
Команда |
Описание |
|
|
Создание массива |
|
Транспонирование массива |
|
|
Нижний индекс |
|
Задание
диапазона |
|
|
Инверсия (обратная матрица) |
|
Скалярное произведение |
|
|
Определитель
матрицы, |
|
Векторное произведение |
|
|
Операция векторизации |
|
Суммирование
|
|
|
Выделение столбца матрицы |
|
Изображение |
Кроме того, матрицы одинаковой размерности можно сложить, вычесть, квадратную матрицу можно возвести в некоторую степень, а два массива − перемножить (если число столбцов первого совпадает с числом строк второго массива). Поэлементное умножение элементов массивов одинаковой размерности или вычисление значений скалярной функции от каждого элемента матрицы возможно с использованием оператора векторизации (таблица 1).
Функции для
работы с векторами и матрицами
Рассмотрим функции, в качестве аргументов которых могут выступать лишь векторы (векторные функции):
· last(v) –
возвращает индекс последнего элемента вектора v;
· length(v) –
возвращает длину вектора v.
· diag(v) – создает
диагональную матрицу, элементы главной диагонали которой формируются из
элементов вектора v.
Из уже существующих массивов можно создавать новые (функции создания массивов):
· augment(A, B, C,…) –
объединяет в один массивы A, B, C и
т. д., имеющие одинаковое число строк (слияние идет бок о бок);
· stack(A, B, C,…) –
объединяет массивы A, B, C и
т. д., имеющие одинаковое число столбцов (слияние массивов идет сверху
вниз);
· submatrix(A, ir, jr, ic, jc) –
возвращает часть массива A, состоящую
из элементов, содержащихся в строках с ir по jr и в столбцах
с ic по jc;
· matrix(m, n, f) −
позволяет создать матрицу размерности m×n, каждый i-й, j-й элемент которой есть функция двух переменных f(i , j), где ![]() и
и ![]() .
.
Для создания матриц специального вида предназначены:
· geninv(A) –
возвращает левую обратную матрицу для A;
· identity(n) – создает
единичную квадратную матрицу размером n×n;
· rref(A) –
ступенчатый вид массива A.
Следующие встроенные функции возвращают значения элементов и специальные характеристики массивов:
· max(A, B, C,…) –
возвращает максимальный по значению элемент;
· min(A, B, C,…) –
возвращает минимальный по значению элемент.
Аргументами функций min и max могут быть не только массивы, но и переменные, числовые значения, строки.
· IsArray(x) –
возвращает значение 1, если x – матрица
или вектор, иначе возвращает 0;
· lookup(z, A, B) – функция
ищет значение z в массиве A и возвращает
элементы массива B, стоящие на
тех же местах, что и z в массиве A (A и B имеют одинаковую
размерность);
· match(z, A) –
возвращает индекс (индексы) нахождения элемента z в массиве A;
· cols(A) –
возвращает число столбцов массива A;
· rows(A) –
возвращает число строк массива A;
· rank(A) –
возвращает ранг массива A;
· tr(M) –
возвращает след (сумму диагональных элементов) квадратной матрицы М;
· mean(A) –среднее
арифметическое значение элементов массива A;
· gmean(A) –
возвращает среднее геометрическое значение элементов массива A. При этом
элементы массива должны быть положительны;
· median(A) –
возвращает медиану элементов массива A;
· mode(A) –
возвращает наиболее часто встречающееся значение элементов массива A.
Для сортировки элементов массивов предназначены:
· sort(v) –
сортировка элементов вектора в порядке возрастания;
· reverse(v) –
перестановка элементов вектора в обратном порядке;
· csort(M, n) –
перестановка строк матрицы M таким
образом, чтобы отсортированным оказался n-й столбец;
· rsort(M, m) –
перестановка столбцов матрицы M таким
образом, чтобы отсортированной оказалась m-я строка.
Примеры к заданию
Задание элементов векторов
Пример 1. Создать вектор-столбец v, состоящий из 5
элементов. Создать вектор w из пяти элементов с использованием ранжированной переменой.
Получить вектор, каждый элемент которого вычисляется по формуле ![]() .
.
Решение.
Напечатаем имя вектора и знак присваивания v :=. Не перемещая курсор, вызовем окно вставки матрицы. Число строк (Rows) зададим равным 5, а число столбцов (Columns) − 1. Нажмем OK. Элементы вектора-столбца введем произвольные, перемещаясь между местозаполнителями с помощью клавиши Tab:
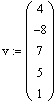
Укажем значение системной переменной ORIGIN равным единице и зададим ряд значений ранжированной переменной для нумерации элементов создаваемых векторов:
![]()
Напечатаем
имя вектора w. Не меняя расположение курсора, нажмем клавишу «[» или
выберем значок ![]() на палитре инструментов Matrix (Матрица), введем нижний индекс i.
Элементы вектора w введем через запятую:
на палитре инструментов Matrix (Матрица), введем нижний индекс i.
Элементы вектора w введем через запятую:
![]()
Создадим вектор, элементы которого
вычисляются по формуле. Напечатаем x, введем
нижний индекс, знак присваивания и расчетную формулу:
![]()
Получим векторы w и x:

Задание элементов матриц
Пример 2. Создать матрицу А
размером 3´2.
Создать матрицу В путем
непосредственного ввода элементов. Получить матрицу С размером 3´2,
каждый элемент которой вычисляется по формуле ![]() .
.
Решение.
Введем имя матрицы и знак присваивания A :=. Не перемещая курсор, вызовем окно вставки матрицы. Число строк (Rows) зададим равным 3, а число столбцов (Columns) − 2. Нажмем OK. Элементы матрицы введем, перемещаясь между местозаполнителями с помощью клавиши Tab:

Зададим системную переменную ORIGIN и ранжированные переменные для нумерации элементов создаваемых массивов:

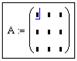
Элементы матрицы B задаются через запятую, а для матрицы C используем формулу. При этом следует указать два индекса:

Вычисление
сумм и произведений элементов массивов
Для
вычисления суммы всех элементов вектора-столбца предназначен оператор
суммирования ![]() ,
находящийся на палитре Matrix (Матрица).
Достаточно задать вектор, отобразить шаблон оператора суммирования и вписать в
знакоместо шаблона имя вектора:
,
находящийся на палитре Matrix (Матрица).
Достаточно задать вектор, отобразить шаблон оператора суммирования и вписать в
знакоместо шаблона имя вектора:

Суммирование или вычисление произведений элементов матриц лучше выполнять с использованием операторов, расположенных на палитре Calculus (Исчисление):

Для суммирования используются шаблоны:
· ![]() , который
заполняется
, который
заполняется ![]() , где i −
переменная, значениями которой являются номера элементов ряда;
, где i −
переменная, значениями которой являются номера элементов ряда;
· ![]() , который
заполняется
, который
заполняется ![]() , где i −
переменная, значениями которой являются номера элементов ряда, n −
константа, обозначающая номер первого элемента, входящего в сумму ряда, m −
константа, обозначающая номер последнего элемента, входящего в сумму ряда.
, где i −
переменная, значениями которой являются номера элементов ряда, n −
константа, обозначающая номер первого элемента, входящего в сумму ряда, m −
константа, обозначающая номер последнего элемента, входящего в сумму ряда.
Например, сумма элементов второй строки и сумма всех элементов матрицы A вычисляются следующим образом:
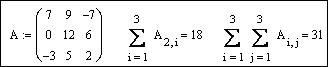
Вычислять произведения помогут шаблоны:
· ![]() , который
заполняется
, который
заполняется ![]() , где i −
переменная, значениями которой являются номера элементов ряда;
, где i −
переменная, значениями которой являются номера элементов ряда;
· ![]() , который
заполняется
, который
заполняется ![]() , где i −
переменная, значениями которой являются номера элементов ряда, n −
константа, обозначающая номер первого элемента произведения, m −
константа, обозначающая номер последнего элемента произведения.
, где i −
переменная, значениями которой являются номера элементов ряда, n −
константа, обозначающая номер первого элемента произведения, m −
константа, обозначающая номер последнего элемента произведения.
Например, произведение элементов третьего столбца и произведение всех элементов матрицы A можно вычислить так:

Обработка
массивов
Пример 3. Ввести массив MS [1..5], состоящий из произвольных чисел, и значение var = 0,95. Для каждого
элемента массива MS вычислить значение RES по формуле ![]() . Подсчитать сумму элементов массива RES. Найти минимальное
значение RES. Отсортировать элементы массива RES по убыванию.
Подсчитать произведение элементов массива RES, стоящих на нечетных
местах. Найти косинус каждого элемента RES.
. Подсчитать сумму элементов массива RES. Найти минимальное
значение RES. Отсортировать элементы массива RES по убыванию.
Подсчитать произведение элементов массива RES, стоящих на нечетных
местах. Найти косинус каждого элемента RES.
Решение.
Зададим порядок нумерации элементов в массивах, начиная с единицы, и ряд значений ранжированной переменной для нумерации элементов создаваемых векторов MS и RES:
![]()
Введем имя исходного массива и знак присваивания. Не меняя положение курсора, выберем кнопку с изображением матрицы дважды и укажем размерность вектора-столбца: Rows – количество строк (5), Columns – количество столбцов (1).
Введем произвольные значения элементов массива MS, используя для перехода к новому знакоместу клавишу Tab или клавиши управления курсором:
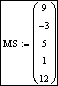
Присвоим значение переменной var:
![]()
Введем формулу для вычисления i-го элемента массива RES:
![]()
Для просмотра результатов в виде таблиц наберем MSi =, RESi =, а для вывода результатов в виде векторов − MS =, RES =:

Вычислим
сумму элементов массива RES. Для этого нажмем на кнопку ![]() на палитре Matrix (Матрица) и введем имя массива. Для
получения результата достаточно нажать «=»:
на палитре Matrix (Матрица) и введем имя массива. Для
получения результата достаточно нажать «=»:
![]()
Для определения минимального элемента используем специальную функцию min:
![]()
Далее отсортируем RES по возрастанию и изменим порядок расположения элементов:

Подсчитать произведение элементов, стоящих на нечетных местах, можно с использованием функции if по формуле:
![]()
Косинус каждого элемента массива RES определяется

Примечания − Функция if в общем виде задается так:
if(условие, выражение_1, выражение_2)
где
· условие −
логическое выражение, заданное с использованием операторов палитры Boolean (Логические);
· выражение_1 −
выражение, которое выполнятся, если условие имеет значение «истина»;
· выражение_2 −
выражение, которое выполнятся, если условие имеет значение «ложь».
Пример 4. Задать матрицу M размером 10×10 по формуле ![]() . Создать подматрицу M1 размером 5×5 из
элементов M, стоящих на пересечении первых пяти строк и пяти последних столбцов.
Найти сумму элементов M1.
Подсчитать произведение элементов матрицы M1 с четной суммой
индексов. Определить минимальный элемент второй строки M1. Создать матрицу M2, каждый элемент которой
– десятичный логарифм соответствующего элемента матрицы M1. Комплексные элементы
матрицы M2 заменить их действительной частью. Найти максимальные элементы в
нечетных столбцах M2. Определить количество отрицательных элементов массива M2. Сформировать вектор z из диагональных элементов
матрицы M2 и найти его модуль. Сформировать вектор w из элементов третьего
столбца M2. Создать матрицу M3 из четных строк матрицы M2 и векторов z и w.
. Создать подматрицу M1 размером 5×5 из
элементов M, стоящих на пересечении первых пяти строк и пяти последних столбцов.
Найти сумму элементов M1.
Подсчитать произведение элементов матрицы M1 с четной суммой
индексов. Определить минимальный элемент второй строки M1. Создать матрицу M2, каждый элемент которой
– десятичный логарифм соответствующего элемента матрицы M1. Комплексные элементы
матрицы M2 заменить их действительной частью. Найти максимальные элементы в
нечетных столбцах M2. Определить количество отрицательных элементов массива M2. Сформировать вектор z из диагональных элементов
матрицы M2 и найти его модуль. Сформировать вектор w из элементов третьего
столбца M2. Создать матрицу M3 из четных строк матрицы M2 и векторов z и w.
Решение.
Определяем переменную ORIGIN и ранжированные переменные для нумерации элементов массивов:
![]()
Задаем матрицу M и ее подматрицу M1, используя встроенные функции:

Вычислим
сумму элементов M1, используя дважды шаблон
суммирования с палитры Calculus (Исчисление):
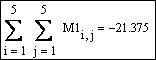
Для подсчета произведения элементов матрицы M1 с четной суммой индексов создаем с помощью функции if вспомогательную матрицу, в которой на указанных местах стоят элементы M1, а на местах с нечетной суммой индексов – единицы. Произведение элементов такой вспомогательной матрицы будет искомым:
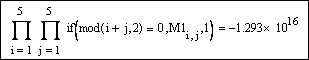
Чтобы определить минимальный элемент второй строки M1, сначала транспонируем
матрицу, затем найдем минимальный элемент второго столбца полученного массива:
![]()
Для
создания матрицы M2 достаточно использовать операцию «векторизации» ![]() :
:
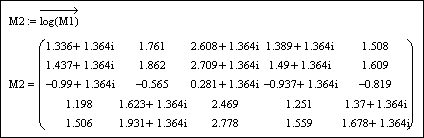
Заменим комплексные элементы матрицы M2 их действительной частью, используя функцию Re(z), возвращающую действительную часть числа z:

Определим максимальные элементы в нечетных
столбцах M2:
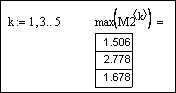
Найдем количество отрицательных элементов M2:
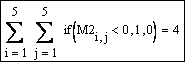
Создадим вектор z из элементов матрицы M2 и найдем его модуль. Сформируем вектор на основе третьего столбца матрицы M2:
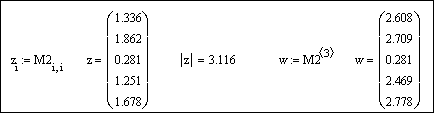
Для создания матрицы M3 можно использовать функцию объединения массивов с одинаковым количеством строк:

Порядок выполнения лабораторной работы
1 Загрузить Mathcad.
2 Сохранить в личной папке на диске z:\ в папке Mathcad\LAB3 новый документ с именем ФИО_3, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3 Вставить текстовую область и ввести в поле документа текст:
Лабораторная работа № 3
Массивы в Mathcad.
4 В новой текстовой области ввести фамилию, имя, отчество и номер варианта.
5 Задать значение системной переменной ORIGIN равным 1.
6 Создать
квадратные матрицы A и B размером
4´4,
используя шаблон ![]() палитры Matrix (Матрица).
палитры Matrix (Матрица).
7 Вычислить
определитель матрицы A с помощью оператора ![]() .
.
8 Найти
матрицу, обратную B, с помощью оператора ![]() .
.
9 Получить
транспонированные матрицы AT и BT, используя оператор .![]() палитры Matrix (Матрица).
палитры Matrix (Матрица).
10 Получить
третий столбец матрицы А, используя
оператор ![]() .
.
11 Получить вторую строку матрицы B, используя последовательно операторы транспонирования и выделения столбца.
12 Найти сумму, произведение, минимальный и максимальный элементы главной диагонали матрицы А.
13 Выполнить задание согласно варианту (таблица 1).
Таблица 1 − Задачи по обработке массивов
|
Вариант |
Задача |
|
|
1 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
2 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
3 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
4 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
5 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
6 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
7 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
8 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
9 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
10 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
11 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
|
12 |
Задать вектор-столбец v, состоящий из четырех
элементов, каждый из которых вычисляется по формуле |
|
Контрольные вопросы
1 Что такое массив?
2 Что такое матрица?
3 Что такое вектор в Mathcad?
4 Какие бывают векторы в Mathcad?
5 Что такое ORIGIN и как она задается?
6 Перечислить способы создания массивов.
7 Перечислить операции для работы с массивами.
8 Перечислить и определить векторные и матричные функции.