Поиск решения средствами Excel

Цель работы – изучение технологии поиска решения в задачах линейного программирования.

Задание

1. Изучить информацию о задачах линейного программирования и о средствах их решения в среде Excel.

2. В соответствии с вариантом задания (документ Var16.doc) подготовить математическую модель задачи и выполнить ее решение с помощью инструмента "Поиск решения".

3. Продемонстрировать решение задачи в среде Excel и интерпретировать полученное решение с точки зрения смысла задачи.

Учебная информация

Пакет поиска решения является надстройкой Excel. Это значит, что в стандартной конфигурации Excel по умолчанию данный пакет не устанавливается. Для того чтобы активизировать его, необходимо выбрать команду Сервис ► Надстройки. На экран будет выведено окно со списком надстроек, установленных в настоящий момент в Excel. Найдите в списке пункт Поиск решения, установите рядом флажок и щелкните на кнопке ОК. Инструмент будет активизирован, и в меню Сервис появится новая команда Поиск решения.

Зачем нужен поиск решения? Если у вас есть некоторый параметр {целевая функция), который зависит от некоторого количества (больше одного) других параметров (переменных), то путем поиска (подбором) решения можно найти такие сочетания переменных, при которых функция принимает заданное значение. При этом можно находить не только заданное постоянное значение, но и минимальное или максимальное значение функции с учетом ограничений, наложенных на значения переменных. Это значит, что путем поиска решения вы можете, например:

- найти такое распределение производственных ресурсов, при котором прибыль будет максимальной;

- найти такое распределение инвестиций, при котором риск будет минимальным;

- находить решения уравнений с несколькими неизвестными с заданными граничными условиями для переменных.

Основные настройки поиска решения выполняются в окне Поиск решения, показанном на рис. 9.7.

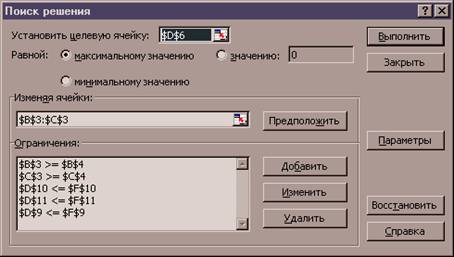
Рис. 9.8. Окно настройки поиска решения

Элементы управления окна Поиск решения перечислены ниже.

В поле Установить целевую ячейку вводится ссылка на ячейку, в которой в результате поиска решения должно быть получено искомое значение.

Группа переключателей Равной позволяет выбрать, что именно должно считаться решением:

• максимальному значению — решением является максимально возможное значение;

• минимальному значению — решением является минимально возможное значение;

• значению — решением является конкретное числовое значение в целевой ячейке, которое нужно ввести в расположенное рядом поле.

В поле Изменяя ячейки необходимо ввести диапазон изменяемых ячеек. Кнопка Предположить позволяет Excel автоматически просмотреть, от каких ячеек зависит конечный результат, и ввести их в поле Изменяя ячейки автоматически.

В списке Ограничения перечислены ограничения, которые накладываются на диапазон изменения переменной. Для того чтобы добавить ограничение к списку, нужно щелкнуть на кнопке Добавить. На экран будет выведено диалоговое окно, показанное на рис. 9.8. В этом окне в поле Ссылка на ячейку нужно ввести ссылку на ту из изменяемых ячеек, для которой вы хотите установить ограничение диапазона изменения значения. В поле Ограничение можно ввести числовую константу, обозначающую границу, или ссылку на ячейку, содержащую эту константу. В раскрывающемся списке нужно выбрать оператор, устанавливающий ограничения диапазона.

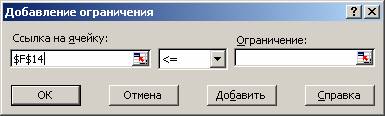
Рис. 9.8. Добавление ограничения

Кнопки Изменить и Удалить служат, соответственно, для редактирования или удаления уже установленных ограничений.

Кнопка Параметры выводит на экран окно настройки параметров поиска решения (рис. 9.9). Рассмотрим окно настройки параметров поиска решения подробнее, поскольку параметры, настраиваемые в этом окне, оказывают серьезное влияние на точность и скорость вычислений.

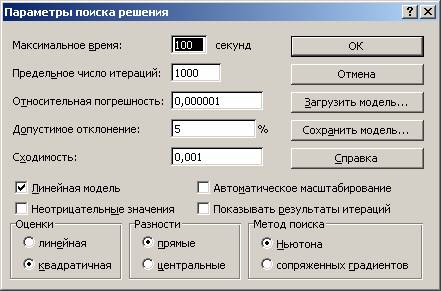
Рис. 9.9. Окно настройки параметров поиска решения

В поле Максимальное время вводится время в секундах, по истечении которого поиск решения будет прекращен даже в том случае, если решение не найдено или не оптимизировано. Допустимые значения — от 1 до 32 767.

В поле Предельное число итераций вводится количество циклов вычислений, после которого поиск решения будет прекращен даже в том случае, если решение не найдено или не оптимизировано. Допустимые значения — от 1 до 32 767.

В поле Относительная погрешность указывается десятичная дробь в интервале от 0 до 1. Чем она меньше, тем выше точность вычислений.

Значение, вводимое в поле Допустимое отклонение, — это величина отклонения в процентах от заданного значения в целевой ячейке. Допустимое отклонение учитывается в том случае, когда на значения в изменяемых ячейках наложено ограничение, согласно которому они могут быть только целыми.

Если за последние 5 итераций относительное изменение значения в целевой ячейке оказывается меньше числа, указанного в поле Сходимость, решение считается найденным.

Флажок Линейная модель нужно установить для ускорения вычислений, если вы решаете линейную задачу оптимизации (задачу, выраженную в линейных уравнениях).

Установка флажка Неотрицательные значения ограничивает диапазон изменения переменных только положительными значениями.

Установите флажок Автоматическое масштабирование, если значения входных переменных и целевой функции значительно (на несколько порядков) различаются по величине, например, вы находите как целевую функцию процентное соотношение, а на входе у вас капитальное вложение в миллиард рублей.

Флажок Показывать результаты итераций нужно установить, если вы хотите видеть весь ход решения, отслеживая значение целевой функции и переменных после каждой итерации.

Группа переключателей Оценки позволяет выбрать метод экстраполяции:

• линейная — экстраполяция дает более точные решения при линейных задачах;

• квадратичная — квадратичная экстраполяция лучше работает при нелинейных задачах.

Группа переключателей Разности позволяет выбрать дифференциалы (производные):

• прямые — прямые производные следует использовать, если анализируемая функция гладкая;

• центральные — центральные производные следует использовать, если в анализируемой функции есть точки разрыва.

Группа переключателей Метод поиска позволяет выбрать метод поиска решения:

• Ньютона — метод Ньютона обеспечивает высокую скорость вычислений, но требует больших затрат памяти;

• сопряженных градиентов — при использовании метода сопряженных градиентов памяти нужно на порядок меньше, но и количество итераций возрастает на порядок.

Кнопки Сохранить модель и Загрузить модель позволяют сохранять установленные параметры прямо в ячейках таблицы, называемых областью модели. Таким образом, вы можете настроить несколько различных наборов параметров и производить поиск одного и того же решения с разными моделями.

Упражнения

1.1. Пример решения уравнения с несколькими неизвестными

В качестве примера проведем поиск решения для уравнения с двумя неизвестными, а также поиск максимального и минимального значений функции с учетом ограничивающих условий.

1. Откройте новый лист в Excel.

2. В ячейку А1 введите значение 2.

3. В ячейку В1 введите значение 1.

4. Для поиска решения используем функцию двух переменных

При задании фиксированного значения z эта функция превращается в уравнение с двумя переменными, поэтому в ячейку С1 введите следующую формулу: = (А1² + В1³)/(В1-А1)

5. Щелкните на ячейке С1 и выберите команду Сервис ► Поиск решения. На экран будет выведено окно Поиск решения, показанное на рис. 9.7.

6. Задайте следующие параметры:

• в поле Установить целевую ячейку введите адрес $С$1;

• в группе Равной установите переключатель значению и введите число 20 в расположенное рядом поле;

• в поле Изменяя ячейки введите диапазон $А$1: $В$1 (это значение будет введено автоматически, если вы щелкнете на кнопке Предположить).

7. Щелкните на кнопке Выполнить.

Решение будет найдено практически мгновенно, что не удивительно: уравнения с двумя переменными либо не имеют решений вообще, либо имеют множество решений, и найти одно из них можно, просто последовательно изменяя значение одной (первой) переменной. Значение (начальное) второй при этом остается фиксированным. Это значит, что решение таких задач зависит от начальных значений. На самом деле, если вы введете в качестве начальных значений переменных в ячейки А1 и В1 значения -1 и 1, вы получите иное решение. Это также говорит о том, что на решение подобного рода задач большое влияние оказывают граничные условия.

Те же самые соображения верны и для поиска максимума и минимума. Поиск этот для большинства функций нескольких переменных должен вестись либо при фиксированном значении всех переменных кроме одной, либо в очень узком диапазоне изменения переменных. Для демонстрации снова введем начальные значения -1 и 1, выберем команду Сервис ► Поиск решения и зададим поиск максимального значения. Вы получите значение целевой функции 2196750 при значениях переменных -2,80932447795488 и -2.80932310682991. Однако, задав начальные значения 5 и 2, вы получите уже иное решение. То есть, когда функция имеет много максимумов, при поиске решения обнаруживается ближайший, и на этом поиск останавливается.

Попробуйте найти решение при наличии ограничивающих значений. Для ячейки А1 это должны быть два значения: >=1 и <=2, — а для ячейки В1 — >=3 и <=4. В этом случае и максимальное, и минимальное значения будут найдены однозначно

1.2. Пример постановки задачи линейного программирования

Акционерное общество производит и реализует оптовыми партиями соответственно по цене 45 руб. и 30 руб. книги и настольные календари. Постоянные затраты общества (управленческие расходы, содержание офиса и т.п.) составляют 202200 руб. в квартал, переменные затраты (стоимость бумаги, услуги типографии и т.п.) – соответственно 15.75 руб. и 12.3 руб. в расчете на одну книгу и один календарь. Налог на добавленную стоимость составляет 16.67 % цены изделия.

Опыт реализации изделий в предыдущие плановые периоды показал, что в течение квартала можно реализовать не более 100000 книг и 40000 календарей.

Требуется на планируемый квартал определить объем производства и реализации изделий (структуру производства и реализации), при котором общество получит максимальную прибыль, а суммарные затраты на производство и реализацию изделий не будут превосходить 2000000 руб.

1.3. Формирование математической модели

Обозначим через х1(х2) неизвестный объем производства и реализации книг (календарей). Суммарные затраты Z на производство и реализацию изделий можно выразить в виде функции неизвестных объемов реализации изделий:

Z(x₁,x₂)=202200+15.75x₁+12.3x₂. (1.1)

Ожидаемая сумма выручки общества V, рассматриваемая как функция неизвестных объемов производства и реализации, составит:

V(x₁,x₂)=45x₁+30x₂. (1.2)

Сумма налога на добавленную стоимость N также выражается в виде функции неизвестных объемов реализации:

N(x₁,x₂)=0.1667*(45x₁+30x₂)=7.5x₁+5x₂. (1.3)

Прибыль акционерного общества P можно записать в виде функции неизвестных объемов x₁ и x₂ следующим образом:

P(x₁,x₂) = V(x₁,x₂) - Z(x₁,x₂ ) - N(x₁,x₂) =

= 45x₁+30x₂ - 202200 – 157.5x₁ - 123x₂ - 7.5x₁ - 5x₂ =

= 21.75x₁+12.7x₂ - 202200. (1.4)

Таким образом, математическая модель ситуации записывается следующим образом:

21.75x₁+12.7x₂-202200 ® max, (1.5)

202200+15.75x₁+12.3x₂£2000000, (1.6)

0 £ x₁ £ 100000, 0 £ x₂ £ 40000. (1.7)

Модель (1.5)–(1.7) можно записать в следующем виде:

21.75x₁+12.7x₂ ® max, (1.8)

15.75x₁+12.3x₂ £ 1797800, (1.9)

x₁ £ 100000, (1.10)

x₂ £ 40000, (1.11)

x₁ ³ 0, x₂ ³ 0.

(1.12)

1.4. Ввод условий задачи

1.4.1. Сформировать таблицу в диапазоне ячеек A1:F11, приведенную на рис. 1.

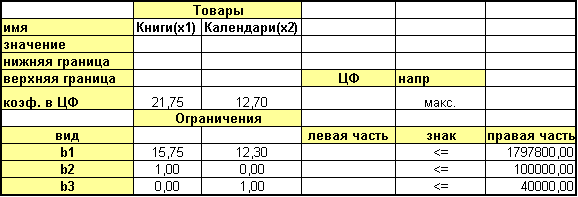
Рис. 1. Таблица для ввода условий задачи линейного программирования

1.4.2. В ячейку D6 ввести формулу =СУММПРОИЗВ(B$3:C$3;B6:C6).

1.4.3. В ячейку D9 ввести формулу =СУММПРОИЗВ(B$3:C$3;B9:C9) и размножить по столбцу в ячейках D10 и D11.

1.5. Решение задачи

1.5.1. В меню выбрать Сервис / Поиск решения. В поле Установить целевую ячейку: набрать $D$6. В поле Равной установить маркер в Максимальному значению.

1.5.2. В поле Изменяя ячейки ввести $B$3:$C$3.

1.5.3. Установить курсор-прямоугольник в поле Ограничения. Нажать на кнопку Добавить. В поле Ссылка на ячейку ввести $B$3. Выбрать знак >=. В поле Ограничение ввести =$B$4. Нажать кнопку Добавить.

1.5.4. В поле Ссылка на ячейку ввести $С$3. Выбрать знак >=. В поле Ограничение ввести =$С$4. Нажать кнопку Добавить.

1.5.5. В поле Ссылка на ячейку ввести $D$9. Выбрать знак <=. В поле Ограничение ввести =$F$9. Нажать кнопку Добавить

1.5.6. В поле Ссылка на ячейку ввести $D$10. Выбрать знак <=. В поле Ограничение ввести =$F$10. Нажать кнопку Добавить

1.5.7. В поле Ссылка на ячейку ввести $D$11. Выбрать знак <=. В поле Ограничение ввести =$F$11. Нажать кнопку OK. В результате диалоговое окно Поиск решения должно быть заполнено также как на рис. 2.

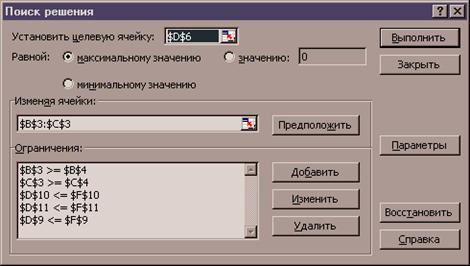
Рис. 2. Диалоговое окно Поиск решения

1.5.8. Нажать кнопку Параметры. Установить линейную модель. Нажать кнопку OK. Нажать кнопку Выполнить.

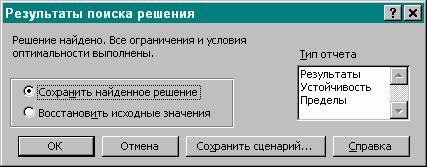
1.5.9. В диалоговом окне Результаты поиска решения, приведенном на рис. 3, установить маркер на опцию Сохранить найденное решение и выбрать в окне Тип отчета – Результаты. Нажать OK.

Рис. 3. Диалоговое окно Результаты поиска решения

1.5.10. В таблице появятся выходные значения, приведенные на рис. 4.

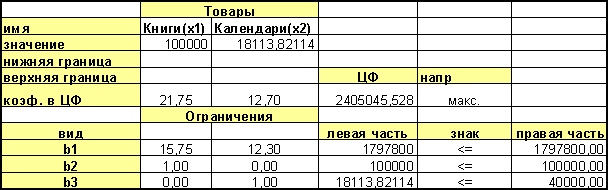
Рис. 4. Выходная таблица решения задачи линейного программирования

Сценарий — это набор значений для изменяемых ячеек, этому набору дано имя.

Благодаря этому средству пользователь таблицы может хранить в ней несколько вариантов расчетов и обращаться к ним при необходимости.

Хотелось бы, однако, иметь перед глазами все сценарии вместе. Для этого в Диспетчере сценариев имеется командная кнопка "Отчет".

Вызовем Диспетчер сценариев и щелкнем по этой кнопке.

Появится диалоговое окно "Отчет по сценарию". На выбор предлагается тип отчета: "структура" или "сводная таблица".